Less-than-four-year Retention Rates

import matplotlib.pyplot as plt
import matplotlib as mpl
import numpy as np
import seaborn as sns
import pandas as pd
import scipy.stats as stats

from tools.utils import filtered_df_two_columns, pearson_corr_coef, prediction_analysis, regression_analysis_results, calculate_MSE

data = pd.read_csv("data/Most-Recent-Cohorts-Institution-filtered.csv").drop('Unnamed: 0', axis=1)

Racial and Ethnic Diversity Analysis

race_columns = ['UGDS_WHITE', 'UGDS_BLACK', 'UGDS_HISP', 'UGDS_ASIAN',
                'UGDS_AIAN', 'UGDS_NHPI', 'UGDS_2MOR', 'UGDS_NRA', 'UGDS_UNKN']
data[race_columns]

	UGDS_WHITE	UGDS_BLACK	UGDS_HISP	UGDS_ASIAN	UGDS_AIAN	UGDS_NHPI	UGDS_2MOR	UGDS_NRA	UGDS_UNKN
0	0.0159	0.9022	0.0116	0.0012	0.0028	0.0008	0.0143	0.0073	0.0440
1	0.5496	0.2401	0.0610	0.0704	0.0024	0.0004	0.0469	0.0232	0.0059
2	0.2550	0.6913	0.0268	0.0034	0.0000	0.0000	0.0000	0.0000	0.0235
3	0.7173	0.0907	0.0599	0.0354	0.0083	0.0010	0.0431	0.0190	0.0252
4	0.0167	0.9265	0.0130	0.0019	0.0017	0.0017	0.0119	0.0155	0.0111
...	...	...	...	...	...	...	...	...	...
6676	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
6677	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
6678	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
6679	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
6680	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN

6681 rows × 9 columns

These columns provide information on the racial and ethnic diversity of undergraduate, degree-seeking students in a particular institutions.

• white (UGDS_WHITE)

• black (UGDS_BLACK)

• Hispanic (UGDS_HISP)

• Asian (UGDS_ASIAN)

• American Indian/Alaska Native (UGDS_AIAN)

• Native Hawaiian/Pacific Islander (UGDS_NHPI)

• two or more races (UGDS_2MOR)

• non-resident aliens (UGDS_NRA)

• unknown (UGDS_UNKN)

We will be using the Simpson’s Diversity Index to describe the Racial and Ethnic diversity of professions schools in the United States.

\[1 - \sum_{i=1}^{n} p_i^2\]

data['diversity_index'] = 1 - data[race_columns].apply(lambda row: row**2, axis=1).sum(axis=1)
data['diversity_index']

0       0.183444
1       0.628836
2       0.455797
3       0.469490
4       0.140635
          ...   
6676    1.000000
6677    1.000000
6678    1.000000
6679    1.000000
6680    1.000000
Name: diversity_index, Length: 6681, dtype: float64

FTL4_institutions = data[data['RET_FTL4'].notnull()][['diversity_index', 'RET_FTL4']]

FTL4_institutions.head()

	diversity_index	RET_FTL4
6	0.430426	0.5915
11	0.661073	0.5538
13	0.588972	0.5961
14	0.527717	0.5449
16	0.478832	0.5357

# less-than-four-year institutions
print(FTL4_institutions['RET_FTL4'].mean(), FTL4_institutions['diversity_index'].mean())

0.6909051969012266 0.47995730161071665

• \(H_0:\) There is no relationship between the retension rate and diversity index at less-than-four-year institutions.

• \(H_1:\) There is no relationship between the retension rate and diversity index at less-than-four-year institutions.

corr, p_value = stats.pearsonr(FTL4_institutions['diversity_index'], FTL4_institutions['RET_FTL4'])
print(corr, p_value)

-0.08259689032835084 4.15791895176101e-06

g = sns.jointplot(data=FTL4_institutions, x='diversity_index', y='RET_FTL4', kind='kde', fill='b')
g.ax_joint.annotate(f'corr: {corr:.2f}, p-value: {p_value:.2e}', xy=(0,1.1))
plt.savefig('figures/RET_FTL4_diversity.png');

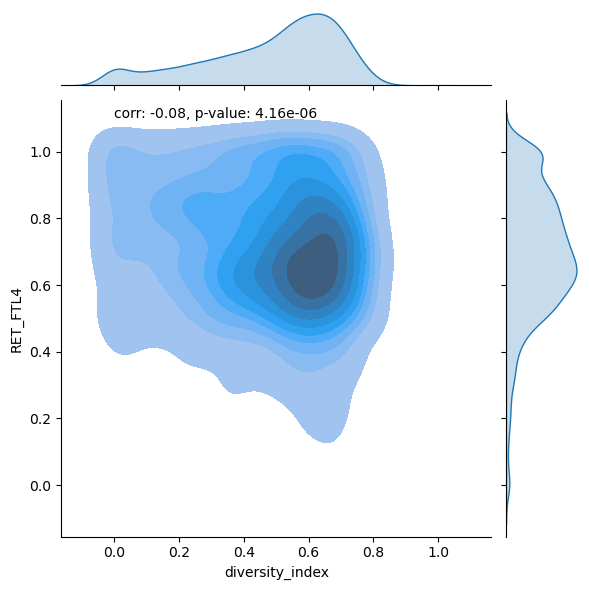
The p-value is very small. This means that we can conclude that there is a relationship between retention rate and diversity index at less-than-four-year institutions. The correlation between diversity index and retention rate is negative. Therefore, we can conclude that as diversity index increases, the retention rate for less-than-four-year institution decreases.

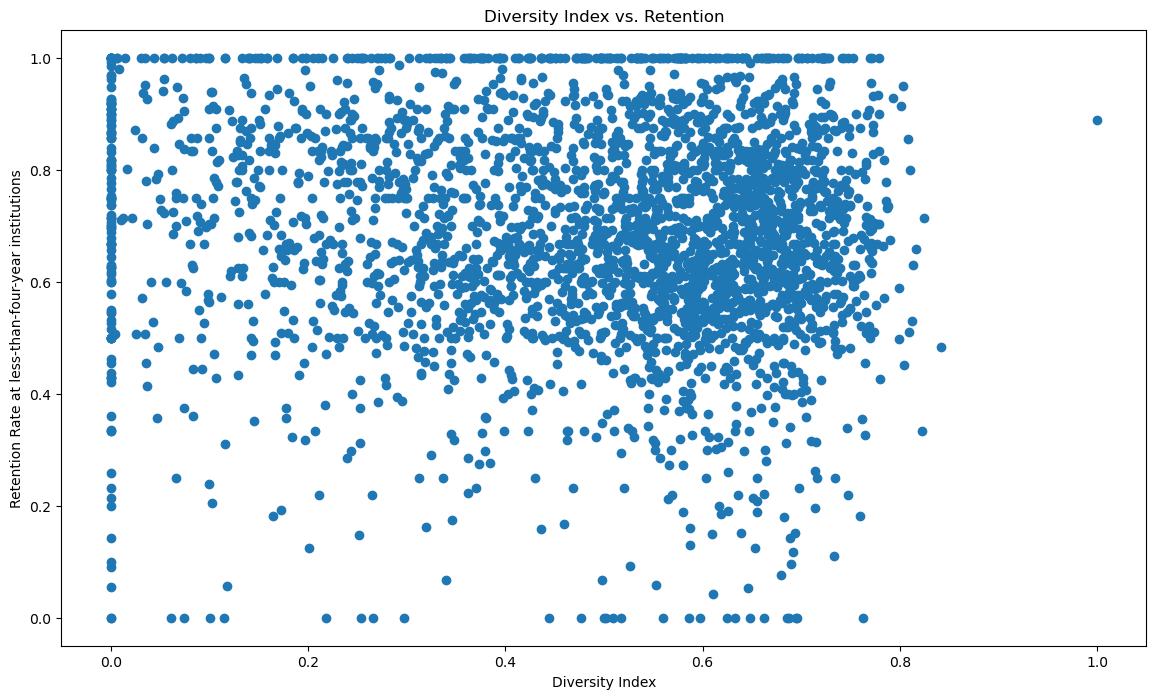
plt.scatter(FTL4_institutions.diversity_index, FTL4_institutions.RET_FTL4)
plt.xlabel("Diversity Index")
plt.ylabel("Retention Rate at less-than-four-year institutions")
plt.title("Diversity Index vs. Retention")
plt.savefig("figures/Diversity_Real_Retention.png")

regression_analysis_results(FTL4_institutions.RET_FTL4, prediction_analysis(FTL4_institutions), 'Diversity_actual_vs_Diversity_predicted.png')

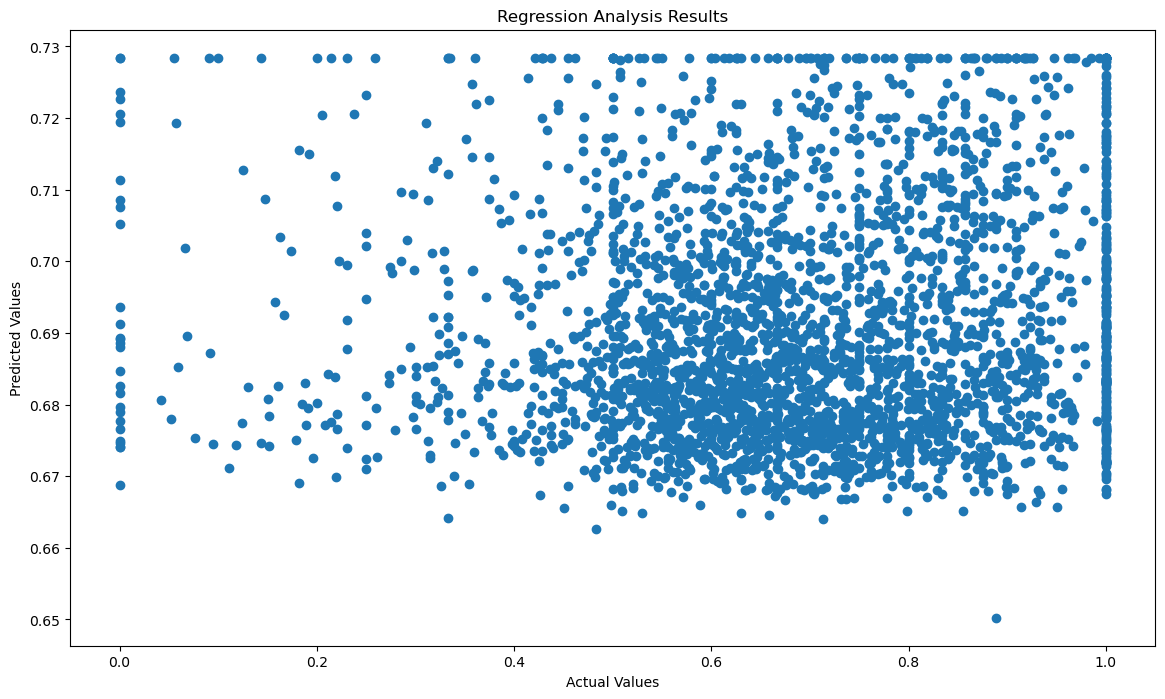
0.006822246291913636

Based on the R^2 value, there does not seem to be a stable prediction of retention values based on diversity index. The R^2 value appears to be too low in order to conclude that there is predictive power.

calculate_MSE(FTL4_institutions.RET_FTL4, prediction_analysis(FTL4_institutions))

0.03870332834271446

However, the MSE value signifies that there is not much error in the predicted values vs the actual values for retention rates.